Sie befinden sich hier
| Artikel | Seite |
|---|---|
| Godehard Murkisch: Herbert Ahues † | 237 |
| Hubert Gockel: Gedanken an Herbert Ahues | 238 |
| Herbert Ahues: Perfect Twomovers | 239 |
| Aktuelle Meldungen | 242 |
| Entscheid im Informalturnier 2013, Abteilung Hilfsmatts in 2 bis 3 Zügen | 245 |
| Entscheid im Informalturnier 2012, Abteilung Märchenschach | 249 |
| 58. Weltkongress für Schachkomposition (WCCC) in Ostróda (Polen), 1. - 8. August 2015 | 252 |
| Ausschreibung Hermann Albrecht 100 Jahre Gedenkturnier der Schwalbe | 254 |
| Bernd Gräfrath: Zweifarbige Zeitverschwendung | 255 |
| Günther Weeth: Anticirce im Retrospiel | 257 |
| Hartmut Laue: Kuckuckseier | 263 |
| Torsten Linß: Zum derzeitigen Wert von Kompositionstiteln | 264 |
| Urdrucke | 265 |
| Lösungen der Urdrucke aus Heft 272, April 2015 | 275 |
| Bemerkungen und Berichtigungen | 295 |
| Schwalbe-Tagung in Aalen, 18. - 20. September 2015 | 295 |
Zweifarbige Zeitverschwendung
Vortrag
beim Schwalbe-Treffen in Aalen, 18. September 2015
von Bernd Gräfrath, Mülheim
Beweispartien unterscheiden sich von sonstigen Retros durch den besonderen Zeitdruck: Die Diagrammstellung muß nicht nur aufgelöst werden, sondern dieses Ziel muß in einer vorgegebenen Zügezahl (in eindeutiger Zugfolge) erreicht werden (die normalerweise die kürzestmögliche sein soll). Umso paradoxer ist es, wenn in Beweispartien Tempospiele gezeigt werden: Trotz des Zeitdrucks sind Wartezüge nötig. Das erklärt sich dadurch, daß eine Seite ein Manöver der anderen Seite quasi abwarten muß, bevor es auflösend weitergehen kann.
Solche Tempospiele sind auch aus Hilfsmatts vertraut: Obwohl die beiden Seiten kooperieren, können trotzdem Wartezüge erforderlich sein. Hier zeigt sich eine gewisse Verwandtschaft der Beweispartien mit dem Hilfsspiel; und charakteristischerweise werden Beweispartien statt "proofgames" manchmal auch "helpgames" genannt. Im Folgenden soll zunächst anhand von drei Hilfsmatts das gemeinte Tempospiel illustriert werden, und zwar jeweils in verschiedenen thematischen Ausprägungen. Der Schwerpunkt liegt danach bei orthodoxen Beweispartien mit gehäuftem Tempospiel. Die größte Herausforderung besteht dabei darin, auf beiden Seiten mehr als einen Tempozug darzustellen: Die Cook-Gefahr ist dabei immens; und umso interessanter ist die Motivation für die Wartezüge.
ZZ1
László Lindner
Tivadar
Kardos
Magyar Sakkvilág 1948
1. Preis Varady-
Gedenkturnier
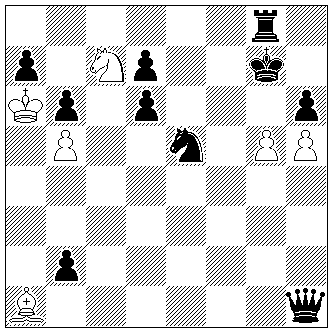
(6+10)
ZZ2
György Páros
Version: Zdravko Maslar
2004 1959
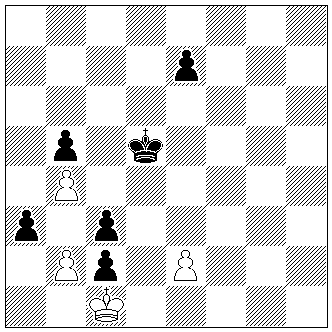
(4+6)
ZZ3
Zoltán Laborczi
The Problemist Supplement
2005
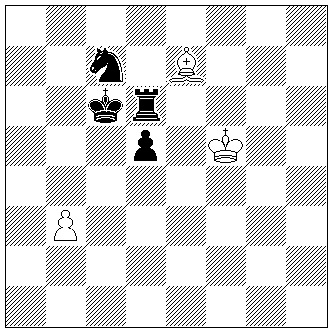
(3+4)
ZZ4
Peter Wong
The Problemist 1995
2. Preis
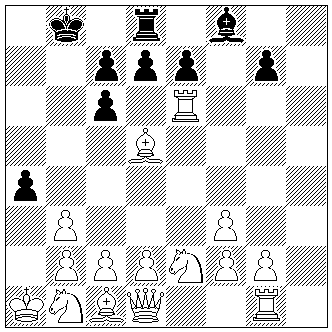
Beweispartie in
21,5 Zügen (15+9)
Die folgende Lösung enthält vier schwarze und einen weißen Tempozug: 1.h3! Sc6 2.h4 Se5 3.h5 Sg6 4.h:g6 f6! 5.g:h7 f5 6.h:g8=L Th3 7.Ld5 Tb3 8.a:b3 f4 9.Ta6 f3 10.Te6 a6! 11.e:f3 a5 12.Lb5 a4 13.Lc6 b:c6 14.Ke2 Lb7! 15.Kd3 La6+ 16.Kc3 Le2 17.S:e2 Db8 18.Tg1 Db4+ 19.K:b4 0-0-0 20.Ka3 Kb7! 21.Ka2 Kb8 22.Ka1. Wenn eine Seite mehr als einen Wartezug hat, besteht die große Gefahr von "oscillation duals"5): Kann statt des thematischen Tempospiels nicht ein einfacher Switchback geschehen? Aber wenn Schwarz hier z. B. Abwartezüge mit dem Sg8 durchführt, dann wird das weiße Spiel gestört: 4.- Sh6? 5.g:h7 Sg8 6.h:g8=L f5 7.Ld5 Th3, und Weiß hat keinen passenden 8. Zug.
ZZ5
Peter Wong
Die Schwalbe 1995
3. Preis
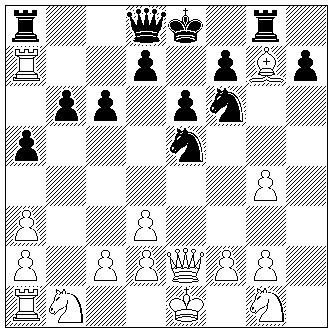
Beweispartie in
15,0 Zügen (15+13)
Nicolas Dupont hat die Herausforderung formuliert, mehr als fünf Tempoverlustzüge in einer orthodoxen Beweispartie zu zeigen.8) Es würde mich freuen, wenn das jemand darstellen könnte. Aber noch gespannter bin ich, ob es irgendwann gelingen wird, zwei Tempozüge der einen Seite mit drei Tempozügen der anderen zu kombinieren. Das wäre wirklich ein Riesenschritt!
Fußnoten:
1) Ich übernehme
die Publikationsdaten aus der PDB (P0522976).
In den folgenden
zwei Büchern sind etwas andere Angaben zu finden: László Lindner,
Mattbilder eines Lebens: Schachliche Selbstbiographie in
drei Sätzen nicht nur für Könner. 66 Jahre Schachkomposition
(Göttingen/Lüneburg: Kuhn/Murkisch-Serie, 1996), S. 264; Walter
Fentze, Tivadar Kardos: 200 ausgewählte Schachprobleme
(Nürnberg: Selbstverlag, 1983), S. 32.
2) Die ursprüngliche Version dieses
Problems ist in der PDB zu finden (P0523080).
Zdravko Maslars
Version entnehme ich folgendem Buch: Thomas Brand, Chris Feather
& Hans Gruber, György Páros: Ein Begründer des modernen
Hilfsmatts (Aachen: Editions feenschach/phénix, 2004), S. 243,
sie ist dort erst-veröffentlicht worden.
3) Thomas Brand empfiehlt für solche Fälle
den folgenden Lackmustest: "Wenn ich den Zug auslassen kann, dann
ist es ein echter Tempozug." Und diesen Lackmustest besteht der
Umwegzug des schwarzen Turms nicht. Ich danke Thomas (der ja
nicht nur ein Retro" , sondern auch ein Hilfsmatt-Experte ist)
für hilfreichen Meinungsaustausch zum Thema Tempospiel. Sein
vorbildlicher Arbeitseinsatz zeigt übrigens überhaupt keine
Anzeichen von Zeitverschwendung!
4)
Zur präzisen Definition des hier gemeinten Tempospiels siehe
Nicolas Dupont, "A compilation of some fascinating open problems
in the Proof Game genre", in: feenschach: zeitschrift für
märchenschach 207 (Mai-Juni 2014), S. 509-529, hier: S. 524.
5) Vgl. dazu Peter Wong, Parallel
Strategy: 156 Chess Compositions (Sydney: Selbstverlag, 2004),
S. 40 ff, sowie auch meinen Aufsatz "Die Rochade in der
Beweispartie als Mittel gegen Oszillationsduale", in: König
& Turm 20 (September 2006), S. 71-72.
6) Ursprünglich erschien die Aufgabe in Die
Schwalbe April 1995; die hier publizierte Neufassung erschien in
Die Schwalbe, August 1996, S. 449.
7) Peter Wong, a. a. O., S. 46.
8) Nicolas Dupont, a. a. O., S. 524.
Impressum Datenschutz
Anschriften: siehe
Vorstand
Internetauftritt: Gerd
Wilts
