Sie befinden sich hier
|
Entscheid
im Informalturnier 2000, Abteilung Zweizüger |
109
114 118 127 129 130 131 134 136 138 145 158 |
| 1. Preis: Nr. 10934 von Wieland Bruch Von Anfang an hat mich diese wunderbare Aufgabe stark beeindruckt. Das Verführungsspiel mit dem wSd6 entfaltet sich mit logischer Klarheit: 1.Sb5? (deckt d4 und droht 2.T:e2) Le3 2.Td4, aber 1.- Ld4! Also 1.Sc4? (deckt e3 und droht 2.Tf4) Ld4 2.Te3 (schöne reziproke Feldbetretung zwischen diesen beiden Phasen), aber 1.- Le3! Durch 1.Sf5? werden die beiden Felder d4 und e3 gedeckt, aber da die Batterielinie nun gesperrt ist, gibt es keine Drohung mehr. Wegen der Deckung der thematischen Felder kann der wT nach 1.- Le3/Ld4 die sL einfach schlagen (also reziproker Mattwechsel in Bezug auf die vorangehenden Phasen), was Schwarz die einzige Widerlegungsmöglichkeit 1.- h5! lässt. Nun ist es wieder absolut logisch, dass Weiß diesen Bauern schlägt: 1.K:h6! (ZZ). Das ist zwar ein ziemlich grober Schlüssel, aber er ist durch die Thematik bedingt. Im Variantenspiel sieht man erstaunlicherweise das Dombrovskis-Thema: 1.- Le3+/Ld4 2.Tf4/T:e2 (dazu noch 1.- Lc5/Lc~/Td1 2.S:c5/Tc3/D:e2). Der wS, der die drei Verführungen ausführt, dient im reellen Spiel nur als Masse, denn ein Bauer könnte auch so gut die 6. Reihe gesperrt halten. Im Gebiet des Hilfmatts würde man diesen Stein wohl als Wiesel betrachten, aber auch Wiesel haben ihrem Platz im ökologischen System der Welt! |
1.
Preis: 10934 Wieland Bruch |
|

|
||
| #2 |
(13+10) | |
|
2.
Preis: Nr. 10615 von Yves Cheylan (John Rice gewidmet) Warten wir ab, was der Preisrichter dazu sagt, hat der Sachbearbeiter bei der Lösungsbesprechung geschrieben. Der Preisrichter sagt: Bravo! Ein erstaunlich kompliziertes Unterfangen: Weiß möchte mit 2.e3 matt setzen, muss daher d3 nochmals decken, aber wie? 1.Le4? sperrt die Linie f4-d4, also 1.- L:f4! 1.Tc3? geht auch nicht, und zwar wegen 1.- S:d2! Nun wird die Aufmerksamkeit des Lösers auf die 5. Reihe gelenkt, wo zwei Felder, c5 und d5, doppelt gedeckt sind. Mit 1.Sce5? verstellt Weiß seinen eigenen Turm, öffnet aber gleichzeitig eine weitere Deckungslinie gegen c5. Schwarz verteidigt sich, indem er die auf das zweite Themafeld (d5) gerichtete Linie sperrt, nicht aber durch 1.- Sb7,c6? (wegen 2.S(:)c6), sondern durch 1.- c6! Die Verführung 1.Sfe5? weist den gleichen Effekt auf: Sperrung der 5. Reihe, Öffnung der Linie g8-d5, Widerlegung durch Sperrung der Linie f8-c5 (1.- Td6!, nicht 1.- Te7? 2.Dd5!). Nur der harmlose Zug 1.Sb2! ist erfolgreich (1.- Te7 2.Td5, 1.- Lg1/L:f4/S:d2 2.D:g1/T:f4/Lc5). Auch der Löser, der nichts von weißen Ekström-Effekten noch Therna-F-Paraden versteht, kann sich an dieser tiefgründigen Aufgabe erfreuen. Nebenbei gesagt: ich danke dem Verfasser für die Widmung, die meine Bewertung keineswegs beeinflusst hat. Als er das Problem einschickte, wusste Yves noch nicht, dass Franz mich zum Richteramt gewählt hatte. |
2.
Preis: 10615 Yves Cheylan |
|

|
||
| #2 |
(13+8) | |
| x |
|
Entscheid
im Informalturnier 2001 der Schwalbe |
|
1.
Preis: 11267 von Camillo Gamnitzer Die herausragende Komposition des Wettbewerbs mit einer Häufung strategischer Elemente, Rückkehr und zyklischem Spiel auf thematischen Feldern. Mit dem verborgenem Schlüssel schwierig zu lösen. Besonders attraktiv ist der Zug 4.Tbh3! - 1.Sc8 droht 2.T:e4+ K:e4 3.Df3+ Kd4 4.Dc3+ Ke4 5.De3+ Kf5 6.g4+ Kf6,K:g4 7.Dg5+ D:g5#, 1.- d5 2.Sc6+ K:c4 3.Sa5+ Kd4 4.Tbh3 a6 5.Sb3+ Kc4 6.Sb6+ K:b4 7.Dd6+ D:d6# |
1.
Preis: 11267 Camillo Gamnitzer Gerald Sladek zum 70. Geb. |
|

|
||
| s#7 |
(13+6) | |
|
2.
Preis: 11078 von Sergej Smotrow Um den Zug Sd4+ zu ermöglichen, wird in einer ästhetischen Stellung das für den Autor typische "Hin und zurück" auf hohem Niveau demonstriert. - Probe 1.Sd4+? L:d4# - 1.Sc7+ Kf6 2.T5g6+ Kf5 3.Tg4+ Kf6 4.Se8+ Ke6 5.Lg8+ Kf5 6.Sd6+ Kf6 7.Tf7+ Ke6 8.Th7+ Kf6 9.Lg5+ Kg6 10.Le3+ Kf6 11.Tf7+ Ke6 12.Sf4+ Ke5 13.Sg6+ Ke6 14.Tg7+ Kf6 15.Se8+ Kf5 16.Sh4+ Ke5 17.Sf3+ Kf5 18.Sd6+ Kf6 19.Tf7+ Ke6 20.Th7+ Kf6 21.Lg5+ Kg6 22.Ld2+ Kf6 23.Tf7+ Ke6 24.Tfg7+ Kf6 25.Se8+ Kf5 26.Lh7+ Ke6 27.Sc7+ Kf6 28.T4g6+ Kf5 29.Tg5+ Kf6 30.Se8+ Ke6 31.Sd4+ L:d4# |
2.
Preis: 11078 Sergej Smotrow |
|

|
||
| s#31 |
(7+9) | |
| x |
|
Entscheid
im Informalturnier 2001 der Schwalbe |
|
Mit 104 Hilfsmatts
war dieser Jahrgang wieder quantitativ gut bestückt. Auch mit
der Qualität der Aufgaben war ich recht zufrieden; es scheint,
dass Achim Schöneberg eine gesunde Vorauswahl vornimmt und
es dadurch den Lösern und Liebhabern (einschließlich
der Preisrichter) leichter macht. a) Hilfsmattzwei-
und -dreizüger |
|
1.
Preis: 11023 von Franz Pachl Sehr gute Nutzung des zusätzlichen Halbzuges zur Voraushinterstellung hinter gleich drei schwarze Steine! (Fast) perfekte Diagonal / Orthogonal-Parallelität in diesem konservativen Stück. Fast - denn 2.d4 geschieht im Gegensatz zu 2.Td4 ohne irgendwelche Auswahl, was mich immer etwas stört. Dennoch klarer Gruppensieger. a) 1.- Dg8 2.d4 L:e6 3.f5 Lc4#, b) 1.- De8 2.Td4 Te6 3. Td7 Te3#. |
1.
Preis: 11023 Franz Pachl |
2.
Preis: 11270 Yves Cheylan |
||

|

|
|||
| h#3 0.1;1.1;1.1 | (5+14) | h#2 | (5+9) | |
| b) |
b) |
|||
| 2.
Preis: 11270 von Yves Cheylan Ich habe gar keine Hemmungen, diesem frechen Stück hier einen zweiten Preis zu geben! Jeweils Turmumwandlungen als reine Tempozüge in einer Patentstellung mit echoartigen Matts durch denselben Springer. Der Clou ist die witzige Zwillingsbildung, die diese paradoxe Verbindung erst ermöglicht. So kann ein Umwandlungszweier auch im 21. Jahrhundert noch originell sein! b) Hilfsmatt vier- und -mehrzüger |
|
1.
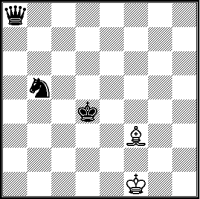
Preis: 11088 von Boris Schochorow Ein merkwürdig unkonventionelles Stück, das mich als Löser faszinierte. Schwarz und Weiß führen einen parallelen eigenartigen Tanz auf, indem jeweils L und S ein Feld betreten, dann verlassen, woraufhin es der "Tanzpartner" betritt. Dass das schwarz-weiße Spiel (bis auf den das Programm eröffnenden kongenialen Schlüssel) nicht miteinander verwoben ist, und auch als zwei Serien nebeneinander verlaufen könnte, stört mich hier gar nicht. Genau das ist ja das Thema, und daher wohl auch die Faszination des Problems, dass das so sieben Einzelzüge lang parallel, schlagfrei und ohne eine schwarze Königsbewegung ablaufen kann. Vor 20 Jahren hätte ich wochenlang nach den NL's gesucht und danach geschrieben: 'todsicher kaputt'. Heute sage ich: 'Erstaunlich'. - 1.Db5 Sc6 (Lc6?) 2.Ld4 (Sd4?) Sb4 3.Lc5 Lc6 4.Sd4 Ld5# und 1.Dc5 Lc6 (Sc6?) 2.Sd4 (Ld4?) Le4 3.Sb5 Sc6 4.Ld4 Sa5#. |
1.
Preis: 11088 Boris Schochorow |
2.
Preis: 11280 Norbert Geissler |
||

|
|
|||
|
h#4
2.1;1...
|
(4+10) | h#7 2.1;1... | (2+3) | |
|
Hier
ist so ein Ding, das früher auch mit nur einer Lösung
fasziniert hätte und auch heute noch manchmal tut - siehe die
M und N. Da gibt es also tatsächlich mit 5 Steinen einen 7-Züger
mit zwei Lösungen und Echomatts in gegenüberliegenden
Ecken. Und keine Langeweile, beide Lösungen haben ihre besonderen
Feinheiten und stehen daher gleichwertig nebeneinander. Riecht nach
PC? Finde ich nicht, auch das nächste Stück trifft meinen
Geschmack. - 1.Ke3 Kg2 2.Sd4 Kh3 3.Kf2 L:a8 4.Kg1 Lg2 5.f3 Lf1
6.Kh1 Kg3 7.Sg1 Lg2# und 1.Kc5 Ke2 2.Kb6 Kd3 3.Ka7 Kc4 4.De4+ Kc5
5.Ka8 Kb6 6.Sa7 Kc7 7.Db7+ L:b7#. |
M
Günter Büsing Hans Gruber Die Schwalbe 8/1992 |
N
Wiktor Scheglow Schachmatnaya Komposizija 1997 1. Preis |
||

|

|
|||
| h#6 | (2+3) | h#7 | (2+3) | |
| 1.f2
La8! 2.Db7+ Kc5 3.f1S Kd4 4.Sh2 Ke3 5.Kh1 Kf2 6.Dg2+ L:g2# |
1.Dg7+
Kf2 2.Se7 Lh1! 3.Dg2+ Ke3 4.Ka8 Kd4 5.Sc6+ Kc5 6.Sb8 Kb6 7.Db7+ L:b7# |
|||
| x |
|
Vorsorge-Staffelung
höheren Grades |
| Eine
Vorplan-Staffelung zweiten Grades liegt nach HALUMBIREK dann vor,
wenn ein Vorplan für den zu sichernden Hauptplan ein neues Hindernis
bewirkt, das vorab einen weiteren Vorplan nötig macht. Ergibt
auch dieser zweite Vorplan für den Hauptplan wieder ein neues
Hindernis, das vorab einen weiteren Vorplan nötig macht, so haben
wir eine Vorplan-Staffelung dritten Grades vor uns und so weiter.
HALUMBIREK sagt: "Je größer der Grad der Staffelung,
desto höher ist die Aufgabe organisiert, desto schwieriger die
Darstellung."
1 bietet
eine Vorplan-Staffelung zweiten Grades mit Lenkungen. Hauptplan
1.S:d5? [droht 2.Sb4+] scheitert an 1.- b4!, nach dem ersten Vorplan
1.Sb4+ T:b4 aber wird der Hauptplan 2.S:d5? durch 2.- Te4! widerlegt.
Das neue Hindernis wurde durch das S-Opfer erzeugt. Daher vorab
der zweite Vorplan zur Aussperrung des sT: 1.h3! [droht 2.h:g4/Tf4]
Ta4!! 2.Tf4 d4! (schwarzer Fluchtschutz) samt 3.Sb4+ T:b4 4.Sd5
T:d5 5.Tf8 6.Tc8. |
1
Stephan Eisert Hans Peter Rehm 4. Pr. Die Schwalbe 1995 Hans Jacob Schudel gew. |
|
 |
||
| #6 | (8+11) | |
| 2
C.G.S. Narayanan 5. Pr. BJM 60-JT 1997 Brian Harley Award |
||
 |
||
| #2 | (8+4) | |
| Vorplan-Staffelungen
mit schwarzen Lenkungen allein sind über diesen dritten Grad
wohl nicht hinausgekommen. Überträgt man nun aber die Auswahllogik
aus 2 auf den Vorplan eines Drei- oder Mehrzügers, so
sind höhergradige Staffelungen durchaus machbar. 3 ist
ein Beispiel für eine Staffelung vierten Grades. Hauptplan 1.Lb5
wäre ein Matt, stünde wSd7 nicht im Wege. Der Vorplan 1.Sf6+
2.Sh7+ Kg8! ergibt ein neues Hauptplanhindemis. Ein weiterer Vorplan
bezweckt daher den Block des Feldes g8 durch den sT. Doch 1.Lf1? [droht
2.Lg2] wird durch 1.- Tg3 2.Tg2 Tc3+! widerlegt. Der Sperrzug 1.Tc4
[droht 2.Lg4] erzielt zwar den Block 1.- Tg8! (2.Tg4 Sg6! - schwarzer
Fluchtschutz) 2.Sf6+ 3.Sh7+ Ke8, verhindert aber jetzt (neues Hauptplanhindernis)
den Mattzug 4.Lb5. Diesen Fehler vermeidet der Sperrzug 1.Lf3! [Tg3
2.Tg2!], wonach 1.- Tg8 als Lenkung nutzbar ist: 2.Sf6+ 3.Sh7+ 4.Lc6. |
| 3
Stephan Eisert 4. Pr. Die Schwalbe 1986 |
4
Herbert Grasemann 1. Pr. Schachmaty w SSSR 1961 Lew Loschinski gew. |
5
Stephan Eisert Hans Peter Rehm Nach Herbert Grasemann Urdruck |
|||
 |
 |
 |
|||
| #4 | (8+7) | #11 | (10+4) | #8 | (11+5) |
| 4 Die Planstruktur ist sehr subtil und komplex. Dem Erfolg des Grundangriffs 1.L:f2 steht das Hindernis (1) Be2 im Weg. 1.e4? (1l. Vorplan) scheitert nur am Patt (Hindernis II). Daher 2. Vorplan 1.e3!?, und nach 1.- T~ folgt 2.e4+ Tf2 2.L:f2#. Neues Hindernis (III) ist 1.- T:d2! (natürlich). Dieses Hindernis wird dadurch beseitigt, dass man den wT weg und wieder zurückspielt. Also 1.d4 Tg2 2.d5+ Tf2 3.Td4 Tg2 4.Tc4+? (z.B.) Tf2. Der Plan 5.e3 Tg2 6.e4+ berücksichtigt alle bisher bekannten Hindernisse 7.e3 Ta2! (das einzige!). Diesen Vorgang nennen wir Planspaltung (Pläne, Spiele, Züge, Die Schwalbe 48, XII/1977, S. 393ff), und würde daher klappen, wenn nicht ein neues Doppelhindemis [IV, V] eingeschaltet worden wäre: 5.e3 Ta2! 6.e4+ T:a7 (IV ist der Angriff auf La7), aber auch 5.- T:f3! 6.e4+ Tf2 7.Td4, Tc5 T:f4!+ (V ist das Schach T:f4+, ohne das Schach ginge 8.Tc,d2+). Daher wird ein weiterer doppelzweckiger Plan nötig, der beide Hindernisse zugleich behandelt: 4.Tb4+ Tf2 5.Tb6! Tg2 6.Ta6+! (Hindernis (IV) beseitigt) Tf2 7.e3 T:f3 8.e4+ Tf2 9.Tb6, und nach 9.- T:f4+ 10.Tf6+ ist Hindernis (V) beseitigt, während nun 9.- Ta2 harrnlos ist, da 10.Tb2+ T:a7 mit 11.Tg2 (Sf3)# beantwortet wird (nach 7.Tg2 ist nur 11.Tg2# vorhanden). Die Zweckökonomie ist (nach Stefan Schneider) trotzdem gewahrt, denn es gibt Zweckkontrollspiele, die eindeutig daran scheitern, dass nur ein Hindernis beseitigt wurde, nämlich 1.d4 2.d5+ 3.Td4 Tg2 4.Ta4+!? und nur (V) bleibt, also 5.e3 T:f3! 6.Td4 nur T:f4+!. Dagegen pariert nur Ta2 (IV), wenn man es in der Lösung etwa mit 6.Tc6+? probiert: Speckmann sagt (W. Speckmann, Das logische Schachproblem, Walter Rau Verlag 1965, S. 26-28) "zweckreine koordinierte Pläne". Die gleichzeitige Ausschaltung zweier Hindernisse ist sozusagen eine der Staffelung entgegengesetzte Manier, mit zwei Hindernissen zu arbeiten. Im Sinn der Staffelung zählt das Doppelhindernis als eines. In dieser Aufgabe ist also eine Vorsorge-Staffelung vierten Grads erreicht. |
| 5
Als wir Grasemanns Meisteraufgabe studierten, haben wir uns gefragt,
weshalb er auf den Vorbau eines kritischen Zugs verzichtet hat. Versetzt
man den wL nach e3 und fügt wBh5, sBh7 hinzu (# 12), so entsteht
die Lösung 1.La7 (1.Lb6? h5!), wobei mit dem Schlüssel ein
weiteres Hindernis (gegen e2-e4) vorab beseitigt wird. Damit wäre
eine Vorsorge-Staffelung fünften Grades erreicht. Diesen Glanzschlüssel
1.La7!! hätte Grasemann sich sicher nicht entgehen lassen. Er
wusste bestimmt, dass das hoffnungslos inkorrekt ist mit 1.S:h1 2.L:f2
3.Lg3. Wir glaubten erst, dass der 10# mit Verzicht auf die logisch
unerhebliche Bahnung des wB für seinen T (also Bd3 nach d5) funktioniert.
Ob Grasemann daran dachte, kann man nicht mehr feststellen. Aber auch
das ist inkorrekt: 1.d6 h6 2.L:f2+ 3.S:h1+, und mit Umwandlung von
Bd6 in D erzielt man rechtzeitig das Matt!! Die Vorplanstaffelung fünften Grades allein mit weißen Führungen gegen fünf Hindernisse (I, II, III, IV, V) ist allerdings durch einen etwas größeren Umbau mit Verzicht auf Hindernis VI und Abkürzung auf 8 Züge erreichbar. In 5 steht für den Hauptplan L:f2# der wBe2 (I) dem wTd2, für den Vorplan 1.e4?? der wLe3 (II) dem wBe2 im Wege. Der wLe3 muß also weg, doch nach 1.Lb6 h6 2.e4?? ist Schwarz patt (III) und nach 2.e3? T:d2 3.e4+ Tf2! fehlt für das Matt L:f2 der wT (IV). Der wT muß also auch weg und nach dem Wegzug des wBe2 wieder zurück, um das Feld f2 zu decken. Anders als bei Grasemann muss Schwarz T:f3 immer unterlassen, denn danach geht Td4-d3-e3-f3+. Der Wegzug des wT schafft ein neues Hinderniss (V): Schach - bei dem Angriff 2.Td4 3.Tb4+ 4.e3 T:c2! 5.e4+ Tf2 6.Td4 geht Tb2! 7.Td2+ T:b6+. Das Schach wird durch eine Auswahl vermieden: der wT muss weiterhin auf die b-Linie, aber der wL nach a7, wo er ohne Schach fällt. Lösung "Take Five" 1.La7!! h6 2.Td4 Tg2 3.Tb4+ Tf2 4.e3 T:c2 5.e4+ Tf2 6.Tb6! Ta2 7.Tb2+ T:a7 8.Tg2#. Unterlässt Schwarz T:c2, so geht der wT wie geplant zurück nach d2, also 4.- Tg2 5.e4+ Tf2 6.Td4! T~ 7.Td2+ Tf2 8.T:f2# "From Russia with Loveday"!. Eine Vorsorge-Staffelung noch höheren Grades ist uns nicht bekannt. |
| x |
|
Endstation
3/4-Zyklus? |
| In
meinem Beitrag "Vor 20 Jahren: Das achte Weltwunder" (Heft
199) habe ich zyklische Umwandlungen im orthodoxen Mehrzüger
angesprochen und ein konstruktiv noch nicht ausgereiftes Beispiel
aus eigener Werkstatt vorgelegt (Nr. 3, Typ DT-TS-SD).
Die folgenden drei Aufgaben dürften besser gelungen sein, aber natürlich drängt sich sofort die Frage nach dem vollständigen zyklischen Babson auf. Zwar sind nicht weniger als sechs mögliche Zyklen denkbar, doch während beim Echo-Babson nicht mehr als zwei Versuche am Patt scheitern müssen, kann sich diese Zahl beim zyklischen leicht auf vier verdoppeln! Man darf also Zweifel haben, ob der große Wurf hier wirklich gelingen kann. Lösungen:
1: 1.c:d7! 1.- c1D 2.d8L! [3.d5#] Da3+ 3.S:a3 K:d6 4.Sf5#, 2.-
D:e3 3.Tf7 D:e1 4.d5#, 2.- Dd1, Dd2 3.d5+ D:d5 4.c:d5# (2.d8D? Da3+
3.S:a3 patt!); 1.- c1L 2.d8S+! Kf6 3.Tg1 L:e3 4.Tf7# (2.d8D? L:e3
3.Tf7 patt!); 1.- c1S 2.d8D! Sb3+ 3.Kb6 S:d4 4.De7/S:d4# (2.d8L?
Sb3+!, 2.d8S+? Kf6 3.Tg1 Sb3+!) -Typ DL-LS-SD. |
| 1 Peter Hoffmann Urdruck |
2 Peter Hoffmann Urdruck |
3 Peter Hoffmann Schach-Aktiv 4/2003 |
|||
 |
 |
 |
|||
| #4 | (14+4) | #4 | (13+9) | #4 | (14+3) |
2: 1.b7! e1D 2.b:c8S! D:e4 3.Le7 ~ 4.Sd6# (2.b:c8D? D:b1!); 1.- e1S 2.b:c8T! Sc2+ 3.T8:c2 (Zz) K:e4 4.Tc3#, 2.- Sd3 3.Te2 ~ 4.Tf8# (2.b:c8D/S? Sc2+ 3.D:e2 patt); 1.- e1T 2.b:c8D! T:e4 3.Df8+ K:g5 4.Le7#, 2.- T:b1 3.Te2 Tc1 4.Df8# (2.b:c8T/S? T:e4 3.Le7 patt!) - Typ DS-ST-TD. 3: 1.f7!
b1D 2.f8S! Db3 3.Se6+ Kc3 4.T:b3#, 2.- D:d3 3.Ld5 D:d2 4.Se6# (2.f8D?
Db4!); 1.- b1S 2.f8L S:a3 3.L:a3 Kc3 4.Lb2# (2.f8D/S? S:a3 3.D:a3
patt!); 1.- b1L 2.f8D! L:d3 3.Dg7 (Zz) K:e4 4.Dg4# (2.f8L/S? L:d3
3.Ld5 patt!) Typ DS-SL-LD. |
| x | |
Buchbesprechungen |
|
| Heft 201, Juni 2003 |
| Harrie
Grondijs (2002). NeverEnding Quest of Type C, Volume B: The Study-as-Struggle.
Mit einem Vorwort von Fred van der Vliet und mit (nachgedruckten)
Aufsätzen von J. Selman jr., A. Rueb, M. Lamare und P. Janse.
ISBN: 90-74827-07-2. 449 Seiten, broschiert, Preis 30,- Euro (incl.
Porto); für 42.- Euro bietet der Autor auch handgebundene Exemplare
an. Auskunft über Bezugsmöglichkeiten beim Schriftleiter
(G. Büsing), der den Kontakt zum Autor vermitteln kann, oder
via www.geocities.com/hhgrondijs, wo auch weitere Informationen abrufbar
sind.
Acht Jahre sind seit der Publikation des ersten Bandes von NeverEnding Quest of Type C von Harrie Grondijs ins Land gezogen (vgl. Besprechung in Die Schwalbe, Heft 148, VIII/ 1994, S. 523-524). Angesichts der Herangehensweise des Autors, wie sie schon damals dokumentiert wurde, überrascht dieser lange Zeitraum nicht, zumal Grondijs auch anderweitig publizistisch aktiv ist. (Er berichtet, von März 1997 bis September 2002 an diesem Band gearbeitet zu haben.) Der zweite Band ist so monumental, wie es der erste war. Nachdem dieser um den Bezug zwischen Studie und Problem ging, wird nun auf 450 eng bedruckten DIN A4-Seiten das"unmittelbare" Geschehen auf dem Brett in der Lösung von Studien analysiert. Der Untertitel "The Study-as-Struggle" beschreibt sehr viel deutlicher als das im ersten Band angekündigte "The Study-as-Game", daß es um die Motivationen und Beweggründe einzelner Züge geht. Während Band 1 visuelle oder logische Muster im Lösungsverlauf untersuchte, rücken nun die "Story" der Lösung, ihre Entfaltung und die detektivische Analyse der einzelnen Bausteine in den Vordergrund. (Für den dritten Band, "The Study-as-Study" ist der Gesamtblick auf das Wesen der Studie als Kunstprodukt angekündigt.) In systematischer, oft geradezu theoretischer Manier, die aber immer mit zahlreichen Diagrammen und mit Analogien aus dem täglichen Leben überaus klar veranschaulicht wird, verknüpft Grondijs seine Abhandlung mit der Darstellung des Entstehens der "realistischen Schule" der Studienkomposition in der Sowjetunion in den 30er Jahren des 20. Jahrhunderts. Einer der zentralen Begriffe hierbei ist der der Domination; anschaulich und doch innovativ zeigt Grondijs auf, daß dieser Begriff eine ganz andere als die gewohnte Bedeutung erhält, wenn bei der Analyse der Lösung von Studien der Blick nur auf die unmittelbare Bedeutung von Zügen gerichtet wird. Überaus nachvollziehenswert ist, wie das Ziel der Domination erreicht wird, wenn das schachliche Geschehen als das Aufeinandertreffen zweier Absichten (der von Weiß und der von Schwarz) interpretiert wird, das dann zu einer gemeinsamen "Aushandlung" des weiteren Vorgehens führt- (Grondijs führt hier das Bild des Boxkampfes an, bei dem es nicht nur darum geht, zu welchem Ergebnis er führt, sondern dessen Verlauf gerade deswegen interessant ist, weil sich die Kontrahenten quasi darüber einigen müssen, wie sie miteinander interagieren - wenn beispielsweise der Boxer mit der geringeren Reichweite dem Gegner den Nahkampf aufzudrängen versucht oder wenn der physisch unterlegene Boxer eine defensive Taktik wählt.) Das Verständnis dieser Interaktion beider Parteien führt gewiß zu einem weitaus tieferen Verständnis des Funktionierens größerer thematischer Muster. Die geradezu enzyklopädische Akribie, mit der Grondijs die Interaktionen klassifiziert und ihr Entstehen schach(studien)historisch untermauert, macht das Buch zu einem schier unerschöpflichen Fundus zur Auseinandersetzung mit dem Kunstschach allgemein. Band 1 zeigte ja explizit, inwiefern reichhaltige Verbindungen zwischen Problernschach und Studienschach gezogen werden können. Für die Inhalte von Band 2 beansprucht Grondijs zwar weitgehend studienspezifische Exklusivität, aber gerade die Interpretation des neudeutschen Mehrzügers durch Eisert & Rehm oder die des Selbstmatts durch Gamnitzer zeigen, daß das anspruchsvolle moderne mehrzügige Schachproblem in gleicher Weise das Aufeinandertreffen zweier (nahezu) gleichwertiger Opponenten kultiviert, die ihre jeweils eigenen Pläne verfolgen und miteinander in Einklang zu bringen haben. Studienhistorisch wird das Entstehen der realistischen Schule der sowjetrussischen Studie in den 30er Jahren des 20. Jahrhunderts (wesentlich initiiert von Kaminer, Herbstmann, Gorgiew und Gurwitsch) interessant aus den Arbeiten von Troitzky und Rinck hergeleitet (die sowohl miteinander verglichen als auch voneinander abgegrenzt werden) und in den Kontext romantischer Studien, die zur gleichen Zeit publiziert wurden, gesetzt. Ein wesentliches Merkmal dieser realistischen Schule ist die "Emanzipation von Schwarz", die das beiderseitige Streben nach Initiative erst ermöglicht. Um einer möglichen Fehlannahme vorzubeugen, sei darauf hingewiesen, daß sich das Buch keineswegs auf die Analyse kurzfristiger Effekte einzelner Schachzüge beschränkt. Vielmehr soll durch die Untersuchung elementarer Wirkweisen das Zustandekommen komplexerer Zusammenhänge überhaupt erklärbar gemacht werden. Dabei gelangt Grondijs zu Analyse-Kategorien, die selbst versierten Lesern bisher wohl unbekannt sind, was ihr Studium umso lohnender macht. Ein Beispiel ist der Effekt des "Tunnelling", mit dem beschrieben wird, wie sozusagen en passant mittels lokaler Ereignisse ein übergeordnetes Ziel erreicht wird. Damit ist dies das Gegenstück zu der neudeutschen Perspektive, in der ein übergeordneter Plan an den Anfang der Lösung gesetzt wird (wie der Betrachter dazu kommt, gerade diesen Plan verfolgen zu wollen, wird in der Regel vernachlässigt) und in der dann lokale Maßnahmen zur Beseitigung von Hindernissen in Gang gesetzt werden (deren Plausibilität durchaus nicht immer einfach ersichtlich ist). Das Studium dieser komplementären Perspektiven ist reizvoll. Eine Vorstellung, wie sie miteinander verknüpft werden können, entwickelt Grondijs im letzten Teil seines Buches, in dem er Progressionen und systematische Manöver analysiert. Hier werden selbst die elementaren Ideen komplex und umfangreich und nähern sich den "großen Ideen" an. Wir können schon jetzt gespannt sein, wie dieser Faden im dritten Band weitergesponnen wird. Wie schon Band 1 liefert auch Band 2 neben den inhaltlichen Gründen auch formale, weswegen sich der Erwerb unbedingt lohnt. Die klare Systematik, das Literaturverzeichnis, das Autorenverzeichnis und viele Graphiken machen das Buch trotz seiner Komplexität und seines intellektuell hohen Anspruchsniveaus sehr gut lesbar. |
| (Hans Gruber) |
Soeben erschienen (Besprechungen folgen in einem der nächsten Hefte): Peter Kniest (†), Hans Gruber, Frank Müller & Rainer Staudte Selbstmatt-Miniaturen Reflexmatt-Miniaturen Band 8 der EDITIONS feenschach-phénix, Aachen 2003, 400 Seiten; John Rice Chess Problem Spectrum - Selected Compositions by John Rice Band 9 der EDITIONS feenschach-phénix, Aachen 2003, 372 Seiten. Beide Bände sind in der von bemd ellinghoven herausgegebenen edlen Serie erschienen: Fadenheftung, schwarzer Ganzleinen-Einband mit Goldprägung. Der Preis liegt jeweils bei 35,- Euro (incl. Porto), zu bestellen bei bemd ellinghoven, Königstr. 3, D-52064 Aachen (e-mail: be.fee@t-online.de). Winfried E. Kuhn Problemschach-Jahrbuch 2002 D Kuhn/Murkisch-Serie Nr. 40, Nightrider Unlimited, Treuenhagen 2003, 416 Seiten, 30,- Euro für die geh. oder 22,- Euro für die kart. Ausgabe. Zu bestellen bei W. E. Kuhn, Grenzstr. 3, 21337 Lüneburg (e-mail: winfriede.kuhn@arcor.de) oder durch Überweisung des Betrags auf Konto G. Murkisch Postbank Hannover, BLZ 25010030, Kt.-Nr. 260 448-305. |
Impressum Datenschutz
Anschriften: siehe Vorstand
Internetauftritt: Gerd Wilts
